Today, instead of going to the computer lab to play Tutpup, we just went into Ms. Magalhaes' room to learn a whole new unit. Mr. Backe gave us 13 words and I THINK we were supposed to define them, but even if we weren't I'll do it anyway :D
Co efficient: Is the number which is multiplied by one or more variables
Variable: Usually letters or other symbols that represent unknown numbers or values
Term: A number or a variable, or the product of numbers and variables
Like Term: Monomials that contain the same variables raised to the same power
Unlike Term: Terms that have variables that are not the same
Degree of Term: The sum of the exponents on the variables in a single term
Degree of Polynomial: The degree of the highest-degree term in a polynomial
Monomial: An algebraic expression containing only one term
Binomial: An algebraic expression that contains two terms that are unlike terms
Trinomial: An algebraic expression that contains three unlike terms
Algebra: A part of math where symbols (usually letters of the alphabet) represent numbers
Constant: In an expression or equation, it has a fixed value and it does not contain variables

To find the degree, you have to find the greatest amount of variables in one term.



REMEMBER TO PLAY TUTPUP!! And ummmm....... PLEASE COMMENT and tell me what I did wrong or something. Hehehheahhah THANKS :D
PS: Colours aren't working D': SORRY!! Trust me it would look WAY prettier with colours :(











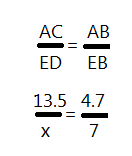









 The next problem is based on a right triangle. Find the a b and c
The next problem is based on a right triangle. Find the a b and c Solve:
Solve:






