4.4 Question 14

LauraKathleen 9-05

" Eliza is building a model of the canvas tent her family uses in Behchoko, NWT. The model will have a peak height of 12 cm. The actual tent floor measures 2.4 m by 3 m. The walls are 1.5 m high and the peak height is 2.4 m.

a) What scale factor will Eliza need to use for her model?

b) The front of the tent is a pentagon. Calculate the dimensions of this polygon on the model.

c) Calculate the other dimensions of the tent model. "

It's always smart to highlight or underline the key points in a question :)

a) To find the scale factor, divide the actual by the reduction. Here's a picture to help:





Step 1: Convert

2.4 m X 100 = 240 cm.

240 cm/ 12 cm = 20 cm

The scale factor for this problem is 20 cm.

b) It gives the bottom length of the pentagon, so naturally, it's the easiest to calculate.

Solution:

3 m/ 100 = 300 cm

300 cm/20 = 15 cm (Divide by 20 because that is the scale factor)

The rest of the sides of the pentagon are the same length, so if you can figure out one, you have them all! For this one, use the Pythagorean Theory.
(a squared + b squared = c squared)






a squared + b squared = c squared

1.5 X 1.5 + 0.9 X 0.9 = c squared

2.25 + 0.81 = c squared

3.06 = c

square root of 3.06 = 1.75 (approx.)

1.75/ 20 = 0.0875 (Divide by 20 because 20 is the scale factor)

0.0875 X 100 = 8.75 cm




Sorry if this is wrong! Please correct me! THANKS :D

Brianna! It's your turn next!

MERRY CHRISTMAS

Mary Jane's Scribepost for December 14, 2010

In today's math class, we started off with playing math wars in which the face cards were equal to 17 and the operation was addition. After that, we then talked about regular polygons.

Regular Polygon: when a shape has equal interior angle and equal side lengths, it is called a regular polygon.


Mr. Backe, then drew a picture that was identified as a five sided regular polygon. The diagram below shows that the two polygons are similar (~). The ratio for each side of the pentagon will have a ratio of 4:8 or 8:4 if the measurements were 4 and 8.



The next shape we were worked with was similar to the shapes in the diagram above although it is connected and some angles are not the same as the one above. The shape looked something like this:




First we put the down the ratios of the corresponding angles and sides which will eventually help solve our problem.

There were two methods we did to find the missing side lengths. The first method was to divide the only corresponding sides that have measurements for both small and big polygon and use that as a scale factor. In this case the ratio is 2/5 and when you divide 2 and 5 you get 0.4 which will then be your scale factor. You then use that scale factor to find the other missing side lengths by multiplying their corresponding side by 0.4. This goes for all of them.

The second method we did was to use a proportional expression to solve the missing side lengths. We used the variable x to represent the missing side lenghts. All the work is shown in the diagram above.




HOMEWORK:

• use the provided diagram above to find the perimeter of the small polygon.
• 4.4 Practise: 3,5,6
• 4.4 Apply: All
• 4.4 Extend: 13-17

*NOTE: click the picture for a larger view.

Connor's Scribepost for December 13, 2010

Today in class we learned more on corresponding angles and how to find the length of sides.

First we corrected the tests.

Then we moved onto corresponding angles.

The corresponding angles are the sides that overlap when the triangle is flipped over the line of reflection.

The two sides that are marked blue are corresponding and the two sides marked yellow are corresponding.

After we reviewed the what corresponding angles are we went onto a quetion involving it.

The question was to find the value of X on the larger triangle.

First you must write the corresponding angles formula.

Next convert the two angle fractions with the measurements given in the question. (Image Below)

Next you must cross multiply.

4.7 (x) = 4.7x

13.7 (7) = 94.5

The answer to this question is x = 20.11

Next we did another question involving overlapping triangles.

The question was asking you to find the height of the ramp if it gives you the height of a support beam.

We need to convert the (cm) to (m)
50cm = 0.5m

Again we must find the side formulas.

(CD/AB) = CE/AE = (DE/BE)

Take the first and third side ^ because that is the measurements that is gives us.

50/x = 175/85

then convert to metres.

0.5/x = 1.75/(1.75+0.85)

Then we cross multiply.

1.75x = 0.5(2.6)

1.75x/1.75= 1.3/1.75

x= o.74m

Then we convert it into cm again which is 74.29cm.

The height of the ramp is 74.29cm.

Sorry if you cant understand some of the math written is hard to understand. I tried the best i could in the time I could. Comment if you have any questions.

The next person for the scribe is Maryjhane

Elijah's Scribepost for December 10 2010

In class today, we classified triangles by its sides, and angles. We also learned more about SAS (side, angle, side).

Classifying Triangles by side:

• Scalene: All Sides are different
• Isosceles: 2 sides are the same.
• Equilateral: 3 sides are equal.

Classifying Triangles by Angle

• Right angle: One angle equals 90°
• Obtuse angle: One angle's greater than 90°
• Acute angle: All angle's are less than 90°
• Equiangular: All angles equal 60°

Other Tringle facts

• All triangles have an interior measure that sums to 180°
• Right triangle:



• Equiangular :
  
  
• Obtuse :
  
• Acute :

SAS (side, angle, side):
If sides and angles are proportional the triangles are similar.

Then we got to solve a problem: Find the b and the h.

Solve:

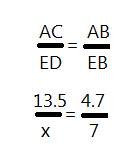
The next problem is based on a right triangle. Find the a b and c

Solve:

Homework :
Extend 18 and 20
Homework book/ Extra practise

Princess' scribepost for December 9, 2010

HELLO(:

So, today in class we learned a little about Similar Triangles. We learned how to determine if two triangles are similar or not. Also, we learned how to use similar triangles to determine a missing side length.

We learned a few terms:
"≅" means "is congruent to"
Congruent- same shape, same size

"~" means "similar to"
Similar- proportional in size

Corresponding Angles/Sides- have the same relative position in a figure









Then we learned that two triangles are similar if:

• two pairs of corresponding angles are congruent (therefore the third pair of corresponding angles are also congruent) WHY? Because the angles of each triangle are equal to 180°.
• the three pairs of corresponding sides are proportional.

After that, we looked at a pair of triangles and figured out if they were similar or not.
*notice that the vertices are always going to be capitalized*






To find out if they were similar or not, we found out if the side lengths were proportional.

Since they are all proportional, the pair of triangles are similar.

Then, we looked at another type or triangle called an Isosceles Triangle.

With this triangle we learned how to find missing side lengths.
For example:
a= 3
e= 6
f= 10
h= ?











We did a few more:
d= 7
h= 5
a= 4
f= ?












A to D= 6
e= 9
f= 12
c= ?
a= ?
h= ?














HOMEWORK:

• Read from this site
• Practice - odds or even
• Apply - odds or even

If I made any mistakes please feel free to comment(:

Allysa's Scribepost for December 6, 2010

In class today, we talked about Scale:Proportional reasoning and we learned how to find a variable's number using "Cross-Multiplication".


A scale is a image:actual.

This is what we started with. I crossed out the A over A because it's not a valid operation and we may not do that.
Also, I put the ticks in the corner of the letter's because they're primes.



Now for the example, it's just like converting a decimal into a fraction. Except your replacing the variable x, into the answer.





Our math teacher also gave us a few questions to practice with. Here are the two:













<-- That is just an easier way to show it.



HOMEWORK: - Read 4.2
- Show You Know(Both)
- Check Your Understanding(1-3)
- Practice(odds or evens)
- Apply(13-16 OR 15-19)
- Extend(20 or 22 and 21)

Some of the questions may show this:
3:5
____
^^You are supposed to measure that line.

And most importantly, there's a TEST ON WEDNESDAY on Scale and Scale Factors.


I choose PRINCESS to do the scribe next!
Thank you for reading my blog! Before you go, please leave a comment behind(:

Mary Jane's Scribepost for December 2, 2010

Hello Everyone! For today's math class, we first had to double the so called "carlos" diagram using tangram shapes. We then went on with talking about dilation and reduction.


Dilation: an enlargement of an object, shape or design. (my own definition, feel free to correct me)


For example:

We also talked about scale factors and scales (ratios).

Scale Factor: The constant factor by which all dimensions of an object are enlarged or reduced in a scale drawing.

Diagram above: It shows the enlargement and the reduction of the square. When the square is enlarged, the area will increase from 36 units(squared) to 144 units(squared) and the side length will increase from 6 units to 12 units. In this case you are what is called doubling (multiplying by 2) and the scale factor is 2. The scale for the enlargement will be 1:2. When the square is reduced, you are basically multiplying the bigger square by 1/2 or 0.5. In this case you are halving and the scale factor is 1/2 or 0.5. The scale for the reduction will be 2:1.

Don't forget to do:

Chapter 4.1 (Page 130-135)
Show You Know (page 132 & 134)
Check Your Understanding (any 2)
Practice: Questions 4,6,7
Apply: Questions 9,11,12
Extend: Questions 14 & 17

Thank you for reading my blog! PLEASE COMMENT! (: